Introdução

O Tonnetz — termo alemão para “rede tonal” — é uma ferramenta visual e conceitual que mapeia relações harmônicas entre notas e acordes no espaço bidimensional. Desde suas primeiras formulações por teóricos como Leonhard Euler no século XVIII até suas interpretações modernas em teoria neo-riemanniana e aplicações digitais em softwares de análise musical, o Tonnetz tem servido como uma poderosa estrutura para entender a organização interna da harmonia na música tonal.

Embora o termo “Tonnetz” só tenha surgido no século XVIII, suas raízes conceituais remontam ao final da Idade Média e à Renascença, quando teóricos já exploravam simetrias e relações interválicas com base em razões numéricas e propriedades acústicas. Este artigo examina o desenvolvimento histórico do Tonnetz, sua construção, aplicações e relevância na música de diferentes períodos — do barroco à música contemporânea.

1. Origens e Fundamentos

1.1 A ideia de relações interválicas

Antes da formalização do Tonnetz, músicos e teóricos buscavam formas de compreender as relações entre sons. Na Grécia Antiga, Pitágoras já havia estudado proporções entre frequências e percebido que intervalos consonantes (como a oitava ou a quinta justa) correspondiam a relações numéricas simples (2:1, 3:2, etc.).

Essas ideias influenciaram a música medieval e renascentista, em que o sistema modal e o contraponto regiam a organização musical. A busca por simetria e equilíbrio harmônico já sugeria uma estrutura subjacente de afinidades tonais, embora não representada graficamente.

1.2 A contribuição de Leonhard Euler

O matemático suíço Leonhard Euler (1707–1783) foi o primeiro a propor uma representação visual dessas relações. Em sua obra Tentamen novae theoriae musicae (1739), ele desenhou um diagrama que dispunha notas musicais de forma a refletir suas conexões harmônicas — particularmente as quintas e terças. Sua “Tonnetz” era um arranjo geométrico em duas dimensões que colocava as notas próximas entre si com base na consonância.

Euler visava mostrar, por exemplo, que o acorde de dó maior (C–E–G) era formado por notas próximas em seu diagrama. Essa proposta antecipava o que hoje chamamos de espaço tonal, um campo teórico no qual acordes e tons podem ser visualizados como vizinhos ou distantes.

2. Construção do Tonnetz

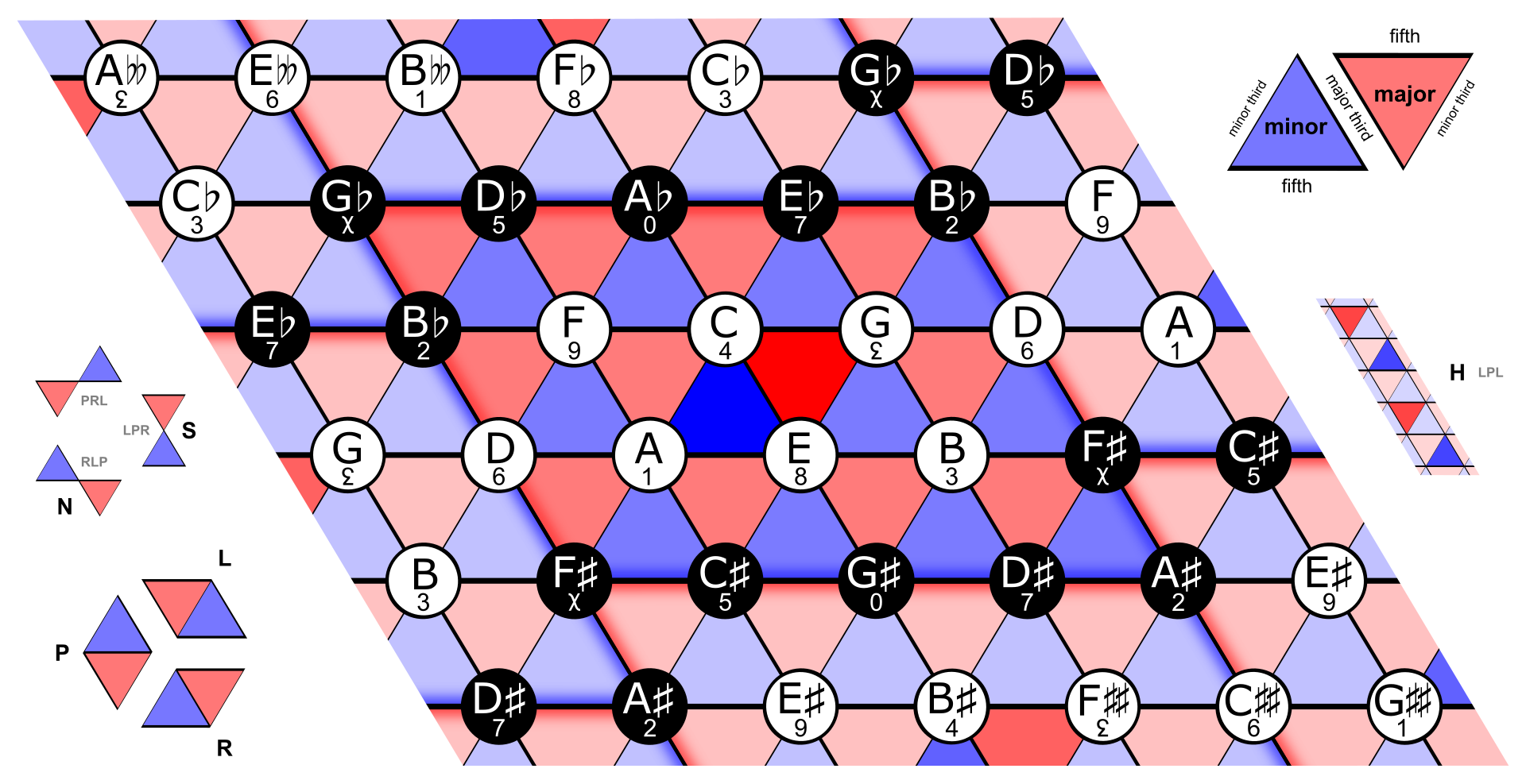
O Tonnetz clássico organiza as notas musicais em uma grade onde:

• O eixo horizontal representa movimentos por quintas justas (por exemplo, C–G–D–A…);

• O eixo diagonal ascendente representa movimentos por terças maiores (por exemplo, C–E–G#…);

• O eixo diagonal descendente representa movimentos por terças menores (por exemplo, C–Eb–Gb…).

Com isso, cada ponto (nota) se conecta com seus vizinhos harmônicos, formando triângulos que representam acordes maiores ou menores.

Um triângulo apontando para cima, por exemplo, representa um acorde maior (C–E–G), enquanto um triângulo invertido representa um acorde menor (A–C–E). Essa representação permite visualizar transformações harmônicas como transposições ou modulações de maneira intuitiva.

3. Teoria Neo-Riemanniana e o Renascimento do Tonnetz

No final do século XIX, Hugo Riemann propôs uma nova abordagem harmônica baseada em transformações entre acordes, particularmente em contextos cromáticos e tonais flexíveis, como os encontrados em Wagner, Liszt e outros compositores românticos.

Três transformações principais definem a base da teoria neo-riemanniana:

• P (Parallel): transforma um acorde maior em seu relativo menor (C → c);

• L (Leittonwechsel): troca a terça de um acorde maior para formar o acorde menor cuja tônica é um semitom abaixo do quinto grau do acorde maior (C → e);

• R (Relative): conecta um acorde maior ao seu relativo menor (C → a).

Essas transformações podem ser visualizadas diretamente no Tonnetz como movimentos entre triângulos adjacentes, o que dá à rede uma funcionalidade analítica poderosa, especialmente em música com cromatismo intenso.

4. Aplicações Musicais

4.1 Análise tonal e cromática

O Tonnetz permite analisar modulações e transformações harmônicas de forma visual. Em peças como o Tristão e Isoldade Wagner, em que a tonalidade se dissolve em um contínuo de cromatismo, a rede tonal ajuda a rastrear conexões entre acordes aparentemente distantes.

Em músicas do século XX (Debussy, Scriabin, Messiaen), o Tonnetz ajuda a entender harmonias não-funcionais, conectando-as por vizinhança interválica em vez de funções tonais tradicionais.

4.2 Música popular e jazz

Compositores e arranjadores de música popular e jazz também se beneficiam do Tonnetz. Ele facilita a compreensão de progressões de acordes por ciclos de quintas, substituições tritonais e reinterpretações modais.

O uso de acordes emprestados (borrowed chords), por exemplo, pode ser visualizado como uma simples transição entre triângulos no Tonnetz, demonstrando como elementos “fora da tonalidade” se conectam a partir de relações de vizinhança harmônica.

4.3 Composição assistida por computador

Softwares como Harmony Space, Tonal Spaces e ambientes de programação musical como Max/MSP ou OpenMusicincorporam versões do Tonnetz para permitir que compositores manipulem acordes e modulações de maneira visual e intuitiva.

A visualização em Tonnetz pode servir tanto para composições atonais quanto tonais, oferecendo novas maneiras de explorar a estrutura do espaço musical.

5. Extensões e variações do Tonnetz

5.1 Tonnetz microtonal

Em contextos microtonais — como em músicas que utilizam escalas de 19, 31 ou 53 divisões por oitava —, versões estendidas do Tonnetz têm sido desenvolvidas. Essas versões incluem mais pontos e conexões, permitindo representar relações harmônicas em sistemas alternativos de afinação.

5.2 Tonnetz tridimensional

Pesquisadores e teóricos também têm explorado versões tridimensionais do Tonnetz, que permitem incluir intervalos como segundas maiores ou trítinos. Um exemplo é o Tonnetz toroidal, que representa a rede como uma superfície contínua (um toro), útil para analisar ciclos harmônicos infinitos.

5.3 Generalizações matemáticas

A intersecção entre matemática e música é intensa no estudo do Tonnetz. Usando teoria dos grafos, topologia e álgebra, estudiosos descrevem a rede como um espaço vetorial onde transformações harmônicas são operações lineares. Isso fornece um arcabouço robusto para aplicações algorítmicas e inteligência artificial aplicada à música.

6. Tonnetz e percepção musical

Além de sua utilidade analítica e composicional, o Tonnetz também se relaciona com a cognição musical. Pesquisas em psicologia da música mostram que ouvintes percebem acordes que estão próximos no Tonnetz como semelhantes, mesmo que estejam distantes na notação tradicional.

Isso sugere que a rede tonal pode refletir não apenas uma estrutura lógica da música, mas também um espaço perceptual, em que a proximidade harmônica é experimentada de forma concreta pelos ouvintes.

Conclusão

O Tonnetz é muito mais do que um simples diagrama. Ele representa uma forma profunda de compreender a música como um campo de relações, em que sons se conectam por afinidade harmônica, simetria interválica e percepção auditiva.

De Euler a Riemann, passando por softwares modernos de composição, o Tonnetz tem sido uma ponte entre o pensamento musical, a matemática e a sensibilidade estética. Seu valor reside tanto na capacidade de descrever o que foi composto quanto de inspirar novas formas de criação.

Em um momento em que a música do mundo inteiro se torna cada vez mais híbrida, cromática e globalizada, o Tonnetz permanece como uma das ferramentas mais poderosas — e belas — para mapear esse universo sonoro em expansão.

---

Se quiser, posso adaptar este artigo para publicação em blog, incluir referências acadêmicas, gráficos com o Tonnetz ilustrado ou transformar em apresentação. Deseja algum complemento?